گیت منطقی چیست؟
گیت های منطقی (Logic Gate) مهم ترین عناصر سازنده تمام مدارات و قطعات دیجیتالی هستند و مبنای گسترش تکنولوژی دیجیتال به حساب می آیند.
گیت های منطقی یکی از مولفه های اصلی الکترونیکی هستند که براساس جبر بولی کار می کنند و برای برقراری هدایت الکتریسیته مورد استفاده قرار می گیرند. این گیت ها برای پیاده سازی توابع منطقی هستند و از بلوک های اساسی سازنده IC ها میباشند.
اصول عملکرد گیت های منطقی
گیت ها به طور کلی دارای یک یا چند ورودی از نوع باینری (دودویی) هستند و با اجرای عملیات منطقی روی آن یک خروجی باینری می سازند.
اصول عملیات گیت ها به این صورت است که مدار فقط با دو سطح ولتاژ کار می کند که این سطوح ولتاژ صفر و یک منطقی نامیده می شوند. زمانی که ولتاژ سطح صفر یا یک به ورودی گیت داده می شود، خروجی گیت براساس ساختار خاص آن یکی از سطوح صفر یا یک خواهد بود.
اعداد باینری و مبنای دو (binary)
اعدادی باینری اعداد ریاضی در مبنای ٢ هستند و داده های آن مقدار ٠ یا ١ می گیرند و قواعد ریاضیاتی بین آنها از جبر بولی پیروی می کند.
این قواعد شامل ارتباطات بین داده های صفر و یکی هستند که براساس دو عملگر (OR) + و (AND) کار می کنند. عملگر OR مشابه عملگر جمع و عملگر AND مشابه عملگر ضرب در مبنای ١٠ هستند اما تفاوت های جزئی بین آن ها وجود دارد.
اساس کار گیت های منطقی
در بخش زیر به بیان قوانین جبر بول و مفهوم هر کدام می پردازیم:
- X + 0 = X
حاصل or شدن هر عددی با ٠ مساوی خود آن عدد است یا به بیان دیگر ٠ عنصر خنثی برای عملگر or است. - X + 1 = 1
حاصل or هر عددی با ١ مساوی ١ می شود. - X+X = X
or هر عدد با خودش، مساوی خودش می شود. - X + not(X) = 1
or هر عدد با متمم خودش مساوی ١ است. - X . 0 = 0
مقدار حاصل and هر عددی با ٠ مساوی ٠ است. - X . 1 = X
با and شدن ١ در هر مقداری پاسخ مساوی همان مقدار است یا به بیان دیگر ١ عضو خنثی در عمل ضرب است. - X . X = X
حاصل and هر عددی با خودش مساوی خودش میشود. - X . not(X)= 0
حاصل and هر عددی با متمم خودش مساوی ٠ خواهد شد. - قانون انجمنی
اعمال عملگر and و or روی حاصل and و or دو عدد دیگر مساوی با and و or شدن آن با هر یک از آن دو عدد است.
A.(B.C) = (A.B).C
A + (B + C) = (A + B) + C
- قانون جا به جایی
جا به جایی عددها در عملگرهای and و or بی تاثیر است.
A.B = B.A
A + B = B + A - قانون توزیعی
مقدار and یک عدد در or شده دو عدد دیگر مساوی با این است که ابتدا عدد اولی در ٢ مقدار دیگر and شده سپس جواب ها or شوند و بالعکس.
x .(y + z) = x . y + x . z
x +(y . z) = (x + y) . (x + z)
ساختار داخلی گیت های منطقی دیجیتال
گیت های منطقی اکثرا با استفاده از دیودها یا ترانزیستورها پیاده سازی می شوند که نقشی مشابه سوئیچ های الکترونیکی دارند. علاوه بر دیود و ترانزیستور، برخی از گیت ها با استفاده از لامپ خلاء، رله الکترومغناطیسی، منطق سیال، منطق هوایی، اپتیک، مولکول و یا حتی عناصر مکانیکی ساخته می شوند.
گیت های منطقی پایه
هفت نوع گیت پایه وجود دارد:
- گیت AND
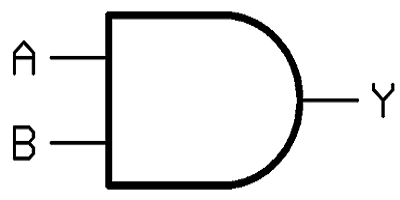
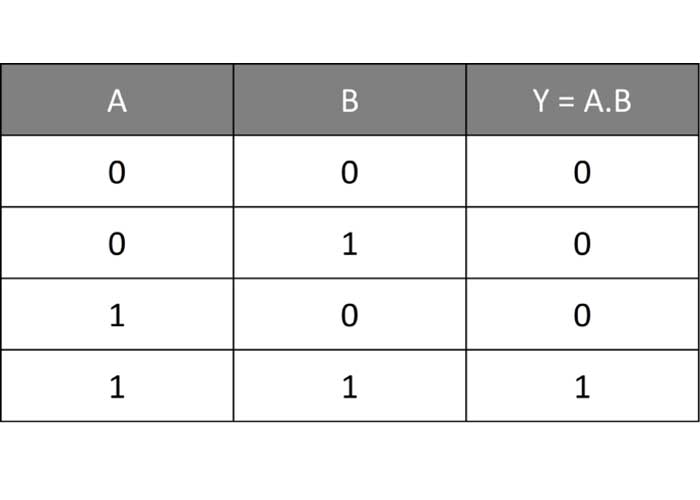
Y = A . B
این مورد یکی از مهمترین گیت های منطقی است که عملکرد آن به این صورت است که اگر هر یک از ورودی ها صفر باشد، خروجی صفر خواهد شد و تنها در صورتی خروجی یک خواهد شد که هر دو ورودی یک باشند.
- گیت OR
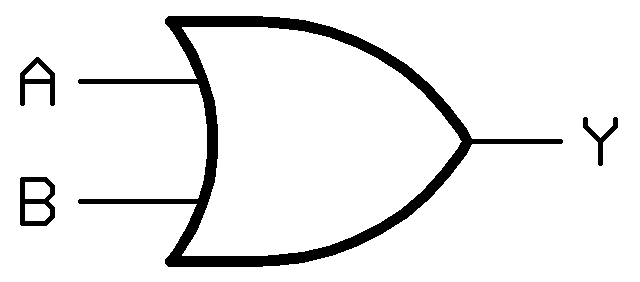
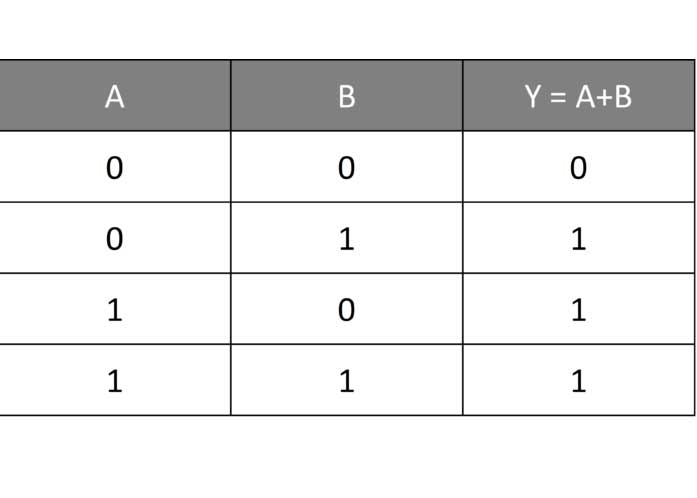
Y = A + B
یکی دیگر از گیت های منطقی پایه ای و پرکاربرد OR است که در آن اگر هر یک از ورودی ها یک باشد، خروجی یک خواهد شد و تنها در صورتی خروجی صفر خواهد شد که هر دو ورودی صفر باشند.
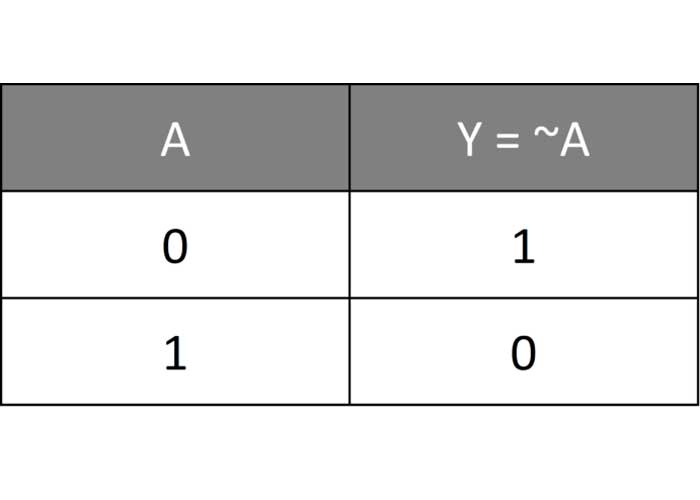
- گیت NOT
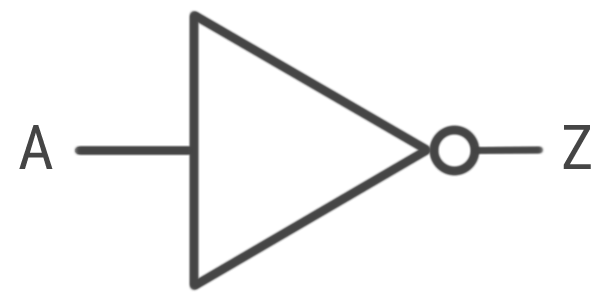
Y = ~A
ساده ترین نوع از گیت های منطقی گیت NOT است منطق ورودی را معکوس می کند، یا به عبارت دیگر متمم هر عدد را می سازد.
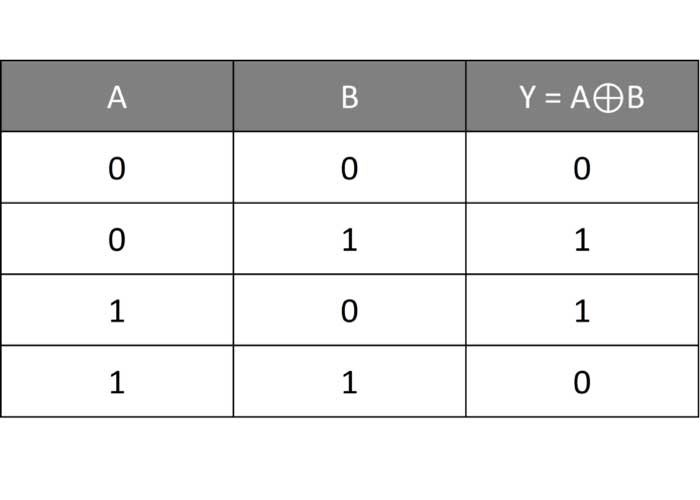
- گیت XOR
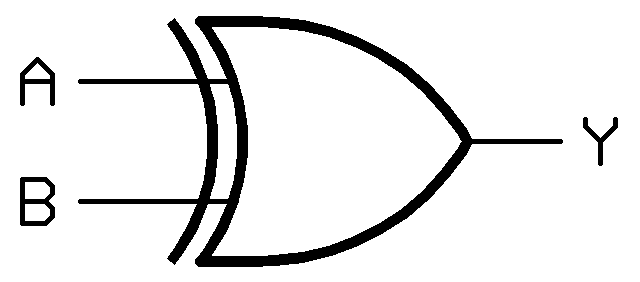
Y = A ⊕ B
گیت XOR یکی از پیچیده ترین انواع گیت های منطقی دیجیتالی است که اگر هر دو ورودی مشابه هم باشند خروجی صفر بوده و اگر متفاوت باشند خروجی یک خواهد بود.
- گیت NAND
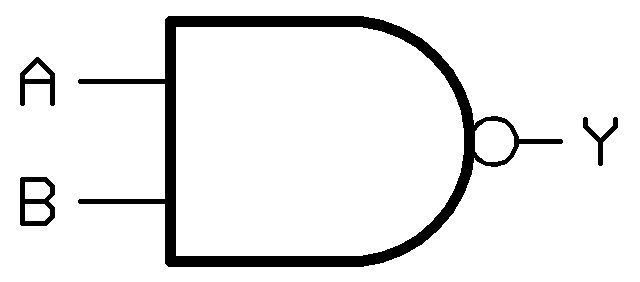
Y = ~(A . B)
گیت NAND یکی از انواع گیت های منطقی سطح بالاست که همان گیت AND است که خروجی آن NOT شده است.
جدول عملکرد این گیت به نحوه زیر است:
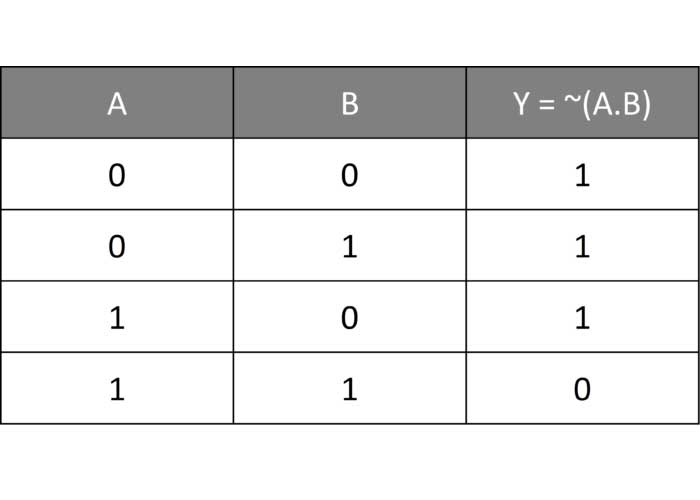
- گیت NOR
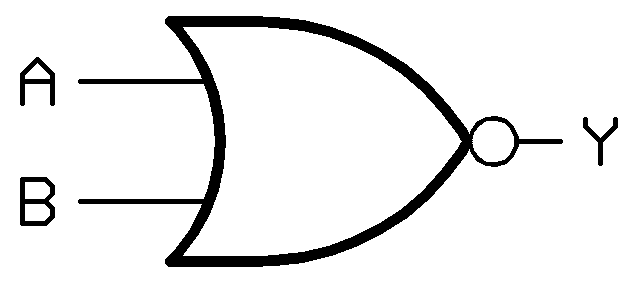
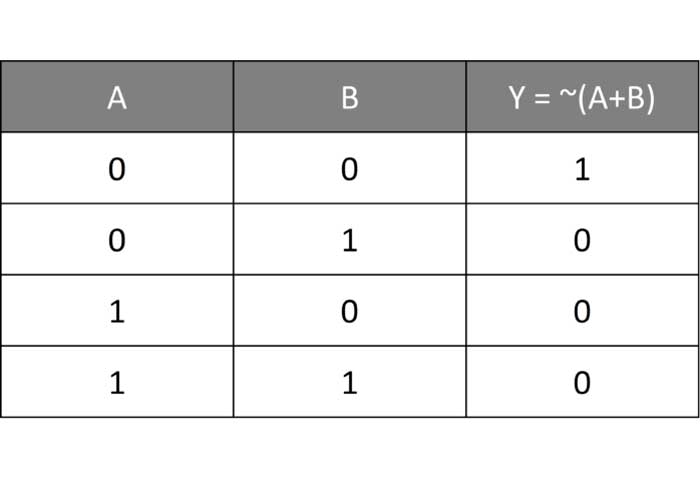
Y = ~(A + B)
یکی از گیت های منطقی سطح بالاتر گیت NOR است که در واقع همان گیت OR بوده که خروجی آن NOT شده است.
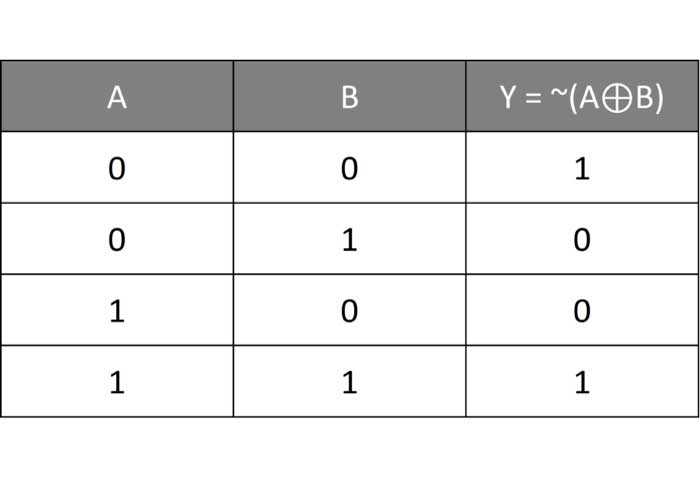
- گیت XNOR
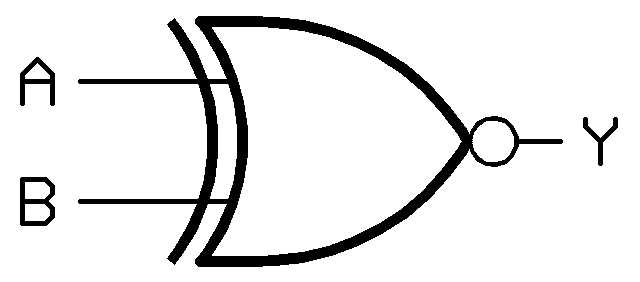
Y = ~(A ⊕ B)
گیت XNOR همان گیت XOR است که خروجی آن NOT شده است.
عملیات های بسیار پیچیده، با بستن مدارهای ترکیب شده از گیت ها قابل اجرا هستند. در تئوری ساخت و طراحی مدار با استفاده از گیت، هیچ محدودیتی برای تعداد آن ها وجود ندارد.











